HPC 矩阵乘法性能基准测试分析

本文将对矩阵乘法在不同硬件和软件实现上的性能表现进行系统性的测试与分析。我将基于一台配备多核CPU和多块GPU的高性能计算节点，从最基础的算法实现开始，逐步考察编译器优化、专用计算库、GPU并行计算以及多设备分布式计算等不同层面的性能差异。通过对比详细的性能数据，揭示硬件特性与软件实现如何共同影响最终的计算效率。

Barkla2 HPC

本次测试所使用的计算节点主要硬件配置如下。中央处理器为两颗英特尔至强金牌5218 CPU，共计32个物理核心，基准频率2.30 GHz，支持睿频加速。该CPU支持AVX-512向量指令集及FMA（融合乘加）操作，这对于加速浮点矩阵运算至关重要。内存系统包含三级缓存：每个核心拥有独立的L1和L2缓存，容量分别为32KB和1MB；所有核心共享23MB的L3缓存。该系统采用NUMA（非一致性内存访问）架构，包含两个NUMA节点，远程内存访问的延迟显著高于本地内存访问。

图形处理器部分包含四块NVIDIA Tesla V100-PCIE-16GB GPU。每块GPU拥有5120个CUDA核心和80个流式多处理器，特别重要的是其内置了640个Tensor Core，能够为半精度（FP16）矩阵运算提供极高的吞吐量。每块GPU配备16GB HBM2显存，可提供约900GB/s的带宽。

设备间的互连拓扑对多GPU性能影响显著。GPU0与GPU1之间，以及GPU2与GPU3之间，均通过高速的NVLink互连（标识为NODE），并分别与两个NUMA节点关联。而位于不同节点上的GPU对（例如GPU0与GPU2）之间则通过相对较慢的PCIe及UPI路径连接（标识为SYS）。这种架构意味着在分布式计算中，算法应尽可能让通信发生在高速互联的GPU对之间，以优化性能。

接下来是使用C++和CUDA实现的基准测试。从最基本的实现开始，逐步增加优化，先在CPU上进行，然后过渡到GPU。这部分将展示如何将硬件特性转化为实际的性能提升。

测试采用的方法很重要。基准测试预先分配了一个随机矩阵池。每次计时迭代会从池中随机选取一对矩阵进行计算。这种设计有助于避免数据因重复使用而过度驻留在高速缓存中，从而能测量出更符合实际应用场景的计算吞吐量。

朴素算法

我们首先分析最基础的矩阵乘法实现，即三重嵌套循环。这是对该算法最直接的翻译。

核心代码示例如下：

void cpu_naive_sgemm(int N, const float* A, const float* B, float* C) {
    for (int i = 0; i < N; ++i) {
        for (int k = 0; k < N; ++k) {
            float temp = A[i * N + k];
            for (int j = 0; j < N; ++j) {
                C[i * N + j] += temp * B[k * N + j];
            }
        }
    }
}

代码采用了 (i, k, j) 的循环顺序。在最内层的 j 循环中，程序连续访问C矩阵的一行和B矩阵的一行。这种顺序的内存访问模式效率较高，因为它符合CPU缓存从内存中连续预取数据块（缓存行）的工作方式。将 A[i * N + k] 存入临时变量 temp，有助于编译器将其保留在寄存器中，从而提升访问速度。

然而，这个实现存在根本性限制。第一，它是完全顺序执行的，仅使用了一个CPU核心。第二，它没有显式利用CPU的AVX-512等向量指令单元。虽然高级编译器在激进优化下可能尝试自动向量化内层循环，但效果通常不如手动优化。

基准测试结果反映了这些限制。当矩阵大小N=128时，平均执行时间约为214微秒，性能大约为20 GFLOPS。当N增大到1024时，执行时间增至185毫秒，性能反而降至约11.6 GFLOPS。这种性能下降是内存层次结构影响的典型表现：较小的矩阵可以大部分保存在缓存中，而较大的矩阵（例如1024x1024的矩阵约占12MB）则超出缓存容量，导致CPU核心需要频繁等待从主内存获取数据。因此，测试跳过了更大的N=2048和4096尺寸。

这个朴素实现设立了一个性能基线，展示了单核CPU在面临内存访问瓶颈时的能力极限。

OpenMP

朴素实现的主要瓶颈是只使用了一个CPU核心。为了利用机器上其他的核心，我们使用OpenMP来实现并行化。OpenMP通过编译器指令来指导循环的并行执行。

在代码上的改动很小，主要是在外层循环前添加一行指令：

void cpu_omp_sgemm(int N, const float* A, const float* B, float* C) {
    #pragma omp parallel for
    for (int i = 0; i < N; ++i) {
        // ... 内层循环保持不变
    }
}

#pragma omp parallel for 这条指令会创建一组线程（通过环境变量 OMP_NUM_THREADS 设置为32，即核心数），并将紧随其后的外层 i 循环的迭代分配到这些线程上执行。由于每个线程负责计算输出矩阵C的不同行，因此不会发生数据竞争。

构建脚本中通过 find_package(OpenMP REQUIRED) 来配置编译环境，这会添加必要的编译选项（例如GCC的 -fopenmp 标志）。

性能提升非常明显。当N=128时，平均执行时间从214微秒减少到15.8微秒，加速约13.5倍。当N=1024时，执行时间从185毫秒减少到5.6毫秒，加速约33倍，这与32核的理想加速比接近。这说明对于大规模矩阵乘法，计算可以很好地被多核心并行处理，线程管理开销相对很小。

需要注意一个关键的代码修复：原始版本曾使用 collapse(2) 子句试图并行化两个外层循环，但这会导致多个线程同时写入C矩阵的同一行，引发数据竞争。修复后仅并行化最外层的 i 循环，确保了每个线程独立写不同的行，从而保证了正确性。

OpenMP版本通过极小的代码改动，显著提升了性能，充分利用了多核CPU的计算能力。但它仍然依赖编译器对内层循环进行向量化优化。

OpenMP+SIMD

OpenMP实现了多核并行，但每个核心内部仍主要执行标量操作。为了进一步提升性能，需要利用CPU的SIMD（单指令多数据）能力。测试平台中的至强金牌5218 CPU支持AVX-512指令集，可以同时处理16个单精度浮点数。AVX512_OMP 基准测试通过使用AVX-512内联函数来显式控制向量化操作。

代码结构与OpenMP版本类似，外层循环由OpenMP并行化。主要区别在于最内层的 j 循环，它被改写为使用AVX-512指令：

void cpu_avx512_sgemm(int N, const float* A, const float* B, float* C) {
    #pragma omp parallel for
    for (int i = 0; i < N; ++i) {
        for (int k = 0; k < N; ++k) {
            __m512 a_val = _mm512_set1_ps(A[i * N + k]);
            for (int j = 0; j < N; j += 16) {
                __m512 b_val = _mm512_loadu_ps(&B[k * N + j]);
                __m512 c_val = _mm512_loadu_ps(&C[i * N + j]);
                c_val = _mm512_fmadd_ps(a_val, b_val, c_val);
                _mm512_storeu_ps(&C[i * N + j], c_val);
            }
        }
    }
}

这段代码的含义如下：

__m512 是包含16个浮点数的512位向量数据类型。
_mm512_set1_ps 将一个标量值复制到向量的所有16个位置。
内层循环步长变为16，因为每条AVX-512指令处理16个浮点数。
_mm512_loadu_ps 从内存加载16个连续的浮点数到向量寄存器中，u 表示允许非对齐地址。
_mm512_fmadd_ps 执行融合乘加操作 a * b + c，这是矩阵乘法的核心运算。
_mm512_storeu_ps 将结果向量存回内存。

从性能结果看，当N=1024时，OpenMP版本耗时约5.6毫秒，而AVX-512版本耗时也在5.6毫秒左右，两者几乎没有差别。这表明，在使用 -Ofast -march=native 编译选项时，现代GCC编译器已经能够自动将OpenMP版本的内层循环向量化，生成的代码效率与手动编写的AVX-512内联函数代码相近。

这个结果说明，对于此类结构规整的循环，编译器能够有效进行自动向量化。手动编写内联函数代码在此案例中并未带来显著的额外性能提升，其主要作用在于验证了编译器优化已达到该算法在CPU上的性能极限。

OpenBLAS

在实际的高性能计算中，通常不会自己实现标准的矩阵乘法，而是使用经过高度优化的库。BLAS（基础线性代数子程序）定义了这类计算的标准接口，OpenBLAS是其中广泛使用的开源实现。

OpenBLAS基准测试将我们之前的三重循环替换为一次函数调用：

cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, N, N, N,
            1.0f, A, N, B, N, 0.0f, C, N);

这一行代码背后是OpenBLAS为各种CPU架构精心优化的计算内核，这些内核通常使用汇编语言编写，并采用了多种高级优化技术：

缓存分块：将矩阵分解成适合CPU各级缓存（L1、L2、L3）大小的块，减少数据在内存和缓存之间的移动。寄存器分块：进一步分块以最大化利用CPU寄存器中的数据，寄存器是速度最快的存储单元。预取：使用特定指令提前将数据从内存加载到缓存，以隐藏内存访问延迟。循环展开：展开内层循环以减少循环控制开销，同时为CPU的乱序执行引擎提供更多指令级并行机会。

性能结果清楚地展示了这些优化的价值。当N=1024时，我们之前最好的手动优化版本（AVX-512+OpenMP）需要约5.6毫秒，而OpenBLAS仅需1.46毫秒，快了约4倍。当N=4096时，OpenBLAS耗时约113毫秒，计算吞吐量达到约1.5 TFLOPS。

这说明，对于实际应用，使用像OpenBLAS这样的优化库通常是正确的选择。它代表了在该CPU架构上，矩阵乘法这一问题所能达到的性能极限。

朴素CUDA

在充分优化了多核CPU之后，为了追求更高性能，我们转向使用GPU进行计算。第一个GPU基准测试是一个“朴素的”CUDA内核实现。它同样是将矩阵乘法算法直接翻译，但采用适合GPU大量核心并行执行的方式。CUDA是NVIDIA的并行计算平台。我们编写称为“内核”的函数，这些函数由GPU上的众多线程同时执行。

朴素的CUDA内核代码如下：

__global__ void cuda_naive_kernel(int N, const float* A, const float* B, float* C) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    if (row < N && col < N) {
        float sum = 0.0f;
        for (int k = 0; k < N; ++k) {
            sum += A[row * N + k] * B[k * N + col];
        }
        C[row * N + col] = sum;
    }
}

其工作原理是：

__global__ 关键字指明这是一个可从CPU调用在GPU上执行的内核。
每个线程通过其所在的块ID和线程ID计算出唯一的行（row）和列（col）索引。这样，每个线程负责计算输出矩阵C中的一个元素。
线程独立计算其对应元素的点积，循环遍历 k，读取A矩阵的一行和B矩阵的一列。

这种方法虽然简单且并行度高，但其内存访问模式存在明显的效率问题。考虑一个线程块中的线程，它们拥有相同的 row 值但不同的 col 值。对于B矩阵的访问，随着 k 变化，线程访问的是 B[k][col_0], B[k][col_1] 等连续的内存地址。这种“合并”访问是高效的，GPU可以通过一次内存事务服务多个线程的请求。

然而，对于A矩阵的访问则效率低下。线程块中拥有相同 col 值但不同 row 值的线程（即同一列的线程），会访问 A[row_0][k], A[row_1][k] 等地址。这些地址在内存中相隔 N 个元素，导致非合并访问，GPU必须为线程束中的每个线程发起单独的内存事务。此外，该算法没有数据重用，每个线程在每次迭代中都直接从GPU的全局内存中重复读取数据，而没有利用更快的片上共享内存。

尽管存在这些内存访问效率问题，GPU庞大的并行计算能力仍然带来了显著的性能提升。当N=1024时，朴素CUDA内核的执行时间约为992微秒。这比我们最好的多核CPU OpenMP/AVX代码（约5.6毫秒）快了约5.6倍，甚至比高度优化的CPU OpenBLAS库（约1.46毫秒）也快了约1.5倍。其计算吞吐量达到约2.1 TFLOPS，超过了之前所有CPU实现的结果。这表明，即使是一个未经过深度优化的GPU内核，凭借其大规模并行硬件特性，也能在处理此类计算密集型任务时展现出优势。

cuBLAS

与CPU上的OpenBLAS类似，在GPU上执行标准线性代数运算，最有效的方式是使用硬件厂商提供的优化库。对于NVIDIA GPU，这个库就是cuBLAS。在基准测试中，我们用一个函数调用替代了自定义的内核。

对于单精度浮点数（FP32）矩阵乘法，调用方式如下：

cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, N, N,
            &a, B, N, A, N, &b, C, N);

cuBLAS的实现采用了深度优化的技术。其核心是一种分块算法：线程块中的线程协同工作，将A和B矩阵的数据块从较慢的全局内存加载到快速的片上共享内存中。然后，线程块内所有线程使用共享内存中的数据执行子矩阵乘法运算，之后再加载下一个数据块。这种设计最大化地复用了已加载的数据，并显著减少了对全局内存的访问流量。此外，cuBLAS的内核使用底层汇编语言（SASS）编写，以精确匹配Volta架构的流水线特性、指令延迟和寄存器文件大小。

性能测试结果如下。当N=1024时，cuBLAS FP32版本的执行时间约为215微秒。这比我们自写的朴素CUDA内核快了约4.6倍，比CPU上的OpenBLAS快了约6.8倍。其计算性能达到约10 TFLOPS，开始接近V100 GPU在FP32精度下的理论峰值性能15.7 TFLOPS。当N=4096时，它保持了较高的效率，性能达到约13 TFLOPS。

V100 GPU的一个关键特性是其Tensor Core单元，这需要通过半精度（FP16）计算来激活。在 cuBLAS_FP16 基准测试中，我们做了两处关键改动：首先，将输入和输出矩阵的数据类型转换为 __half（即FP16）；其次，调用函数启用Tensor Core计算模式：

cublasSetMathMode(cublas_handle, CUBLAS_TENSOR_OP_MATH);

随后，调用 cublasHgemm 函数执行计算。

启用FP16和Tensor Core带来了显著的性能提升。当N=1024时，执行时间降至约50微秒，比FP32版本的cuBLAS快了约4.3倍，性能超过42 TFLOPS。当N=4096时，性能达到约87 TFLOPS。这与32核CPU上高度优化的OpenBLAS相比，提升了近70倍。V100的Tensor Core专为深度学习和科学计算中常见的密集矩阵运算设计，能够在可接受的精度损失下，提供数量级级别的性能提升。

MPI + cuBLAS

为了将矩阵乘法扩展到四块GPU，我们使用工业标准方案MPI（消息传递接口）。在这个基准测试中，我们将每块GPU视为一个独立的计算单元，并由一个独立的CPU进程管理，即“每GPU一进程”模型。这种模型避免了在单个进程中管理多GPU的复杂性。

初始化阶段的关键步骤是确保每个MPI进程绑定到特定的GPU。如果所有进程都试图使用同一块GPU，性能会严重下降。代码通过计算local_rank（本地排名）来实现这一点：

MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &mpi_rank);
MPI_Comm_size(MPI_COMM_WORLD, &mpi_size);

// 创建一个仅包含同一物理节点上进程的通信器
MPI_Comm node_comm;
MPI_Comm_split_type(MPI_COMM_WORLD, MPI_COMM_TYPE_SHARED, mpi_rank, MPI_INFO_NULL, &node_comm);
MPI_Comm_rank(node_comm, &local_rank);

// 将当前进程绑定到特定的 GPU
int num_devices;
cudaGetDeviceCount(&num_devices);
CUDA_CHECK(cudaSetDevice(local_rank % num_devices));

这段代码的逻辑是：首先，MPI_Comm_split_type将共享内存（即同一台服务器上）的进程分组。然后，每个进程获取一个local_rank（0、1、2或3）。最后，通过cudaSetDevice(local_rank)将进程绑定到对应的GPU。这样建立了进程与GPU之间一对一的映射，这对性能很重要。

在MatrixPool结构体中，内存分配使用标准的CUDA调用，因为MPI模式下每个GPU的内存是独立的：

void* alloc_mem(size_t bytes) {
    void* ptr;
    // MPI 模式下的标准 CUDA 分配
    CUDA_CHECK(cudaMalloc(&ptr, bytes));
    return ptr;
}

基准测试循环的核心是测量四块GPU并行计算的时间。在MPI版本中，同步由CPU处理。我们使用MPI_Barrier确保所有进程在开始计时前准备就绪，并在计算结束后再次同步以确定所有进程都已完成：

// 1. 同步所有进程（CPU 在此等待）
MPI_Barrier(MPI_COMM_WORLD);
double start = MPI_Wtime();

// 2. 异步启动 GPU 上的计算内核
if (use_fp16) {
    cublasHgemm(cublasH, CUBLAS_OP_N, CUBLAS_OP_N, ...);
} else {
    cublasSgemm(cublasH, CUBLAS_OP_N, CUBLAS_OP_N, ...);
}

// 3. 等待本地 GPU 完成工作
CUDA_CHECK(cudaDeviceSynchronize());

// 4. 再次同步所有进程，以测得最慢进程的时间
MPI_Barrier(MPI_COMM_WORLD);
double end = MPI_Wtime();

这段代码显示了同步开销。cublasSgemm或cublasHgemm是非阻塞调用，会立即返回，而GPU在后台计算。cudaDeviceSynchronize()使CPU等待其本地GPU完成任务。最后的MPI_Barrier确保我们测量的是所有进程中最后一个完成的时间。例如，如果GPU0在10毫秒内完成，而GPU3花了11毫秒，那么报告的时间就是11毫秒。这对于分布式算法是必要的，因为整个系统的速度取决于最慢的组件。

从的数据来看，MPI实现在矩阵大小8192下，FP16精度性能达到81.68 TFLOPS。这表明，与大规模矩阵乘法的计算负载相比，MPI_Barrier带来的同步开销很小。GPU将绝大多数时间花在cublasHgemm计算上，使得这种方案对于计算密集型任务非常高效。

NVSHMEM

NVSHMEM 提供了一种不同的并行编程方式。与MPI中独立进程相互发送消息不同，NVSHMEM 建立了一个全局地址空间。这使得运行在GPU0上的CUDA内核能够直接访问GPU1上分配的内存，利用高速NVLink互连，而不需要CPU参与数据传输。

我们仍然使用MPI来启动环境，但需要额外初始化NVSHMEM运行时，以便将各个GPU的内存映射成一个统一视图：

// 初始化 NVSHMEM，使用 MPI 交换设置信息
MPI_Comm comm_world = MPI_COMM_WORLD;
nvshmemx_init_attr_t attr;
attr.mpi_comm = &comm_world;
nvshmemx_init_attr(NVSHMEMX_INIT_WITH_MPI_COMM, &attr);

最重要的区别在于内存分配。我们不能使用 cudaMalloc，而是使用 nvshmem_malloc。这个函数从称为“对称堆”的特殊区域分配内存：

void* alloc_mem(size_t bytes) {
    void* ptr;
    // NVSHMEM 分配：这块内存现在可以被其他 GPU 访问
    ptr = nvshmem_malloc(bytes);
    return ptr;
}

当在GPU0上调用 nvshmem_malloc 返回指针 ptr 时，这个指针映射到GPU0上的物理内存地址。由于对称堆的特性，其他GPU（如GPU1）也知道如何访问这个地址对应的数据。虽然在这个基准测试的计时循环中没有显式使用数据传输操作（如 nvshmem_put 或 nvshmem_get），但使用 nvshmem_malloc 确保内存布局已经为这类操作做好了优化。

同步机制也从CPU转移到了GPU（或NVSHMEM运行时）。我们不再使用 MPI_Barrier，而是使用 nvshmem_barrier_all：

// 1. 跨所有 GPU 的全局屏障
nvshmem_barrier_all();
double start = MPI_Wtime();

// 2. 计算
if (use_fp16) {
    cublasHgemm(...);
}

// 3. 等待本地 GPU
CUDA_CHECK(cudaDeviceSynchronize());

// 4. 再次全局屏障
nvshmem_barrier_all();
double end = MPI_Wtime();

结果显示，NVSHMEM FP16在矩阵大小8192下的性能为79.58 TFLOPS，与MPI的81.68 TFLOPS几乎相同。这表明，对于纯计算密集型任务（如矩阵乘法，计算过程中GPU之间不需要交换数据），MPI和NVSHMEM的性能差异很小，因为瓶颈在于计算本身。

接下来，我们转向使用Python实现的基准测试。尽管Python作为一种解释型语言通常被认为速度较慢，但在科学计算领域，通过调用底层高效库，它同样能获得出色的性能。对于许多研究人员和数据科学家来说，Python提供了更快的开发速度和更简洁的代码，而性能关键的计算则交由后端的优化库完成。我们将首先分析基于CPU的NumPy，之后再讨论基于GPU的CuPy和JAX。

NumPy

NumPy是科学计算中不可或缺的基础库，它提供了多维数组对象和大量数学函数。其性能的关键在于，虽然用户使用Python编写代码，但NumPy会将矩阵乘法等计算密集型操作，委托给底层的优化库（如OpenBLAS或Intel MKL）执行。这些库与我们之前在C++基准测试中使用的相同。

进行矩阵乘法的Python代码非常简洁：

import numpy as np
result = np.matmul(a, b)

在这行代码背后，NumPy实际上调用了BLAS库中的cblas_sgemm函数。因此，对NumPy的基准测试，本质上测试的是其链接的BLAS库的性能。测试脚本通过设置环境变量（如OPENBLAS_NUM_THREADS）来确保使用全部CPU核心。

测试脚本采用了pytest-benchmark框架，并使用DataPoolCache预先生成矩阵池。在计时开始前，数据（对于GPU库还包括传输到设备的数据）已准备就绪。这样，计时的run_one_round函数只测量核心计算时间，排除了数据初始化和传输的开销，使得与C++基准测试的比较更为公平。

查看性能数据，当N=1024时，NumPy的平均执行时间为1.74毫秒；当N=4096时，为89.3毫秒。这与C++ OpenBLAS的结果（N=1024时为1.46毫秒，N=4096时为98.8毫秒）非常接近。微小的差异可能源于测试环境或具体配置，但总体表明NumPy的性能几乎完全取决于其底层BLAS库的效率。Python层面的开销极小，在计算时间较长时可以忽略不计。这体现了“双语言”策略的优势：用Python进行高层逻辑组织和快速原型设计，而性能关键的计算则由高效的低级语言库完成。

CuPy

CuPy可以被视为“GPU上的NumPy”。它提供了与NumPy几乎相同的编程接口，但其数组对象（cupy.ndarray）位于GPU显存中，其运算由CUDA内核执行。对于矩阵乘法，CuPy在底层会自动调用相应的cuBLAS函数。

使用CuPy的流程简单直接。开发者可以基于现有的NumPy代码，稍作修改即可在GPU上运行。基准测试代码中的关键步骤如下：

在CPU上创建NumPy数组。
使用 cupy.asarray() 将数组传输到GPU显存。
使用CuPy的 matmul 函数执行计算，其语法与NumPy相同。

示例代码：

import cupy as cp
# a_cpu 和 b_cpu 是 NumPy 数组
a_gpu = cp.asarray(a_cpu)
b_gpu = cp.asarray(b_cpu)
# 这是被计时的部分
result_gpu = cp.matmul(a_gpu, b_gpu)
# 阻塞直到GPU完成
cp.cuda.Stream.null.synchronize()

基准测试脚本的 DataPoolCache 在计时开始前已经完成了 asarray 的数据传输，因此我们只测量 cp.matmul 的调用时间，这本质上是对 cublasSgemm 或 cublasHgemm 的封装。

性能结果方面，cupy_fp32 的结果与C++ cuBLAS FP32结果相似：

当N=1024时，Python/CuPy耗时294微秒，C++/cuBLAS耗时215微秒。
当N=4096时，Python/CuPy耗时10.49毫秒，C++/cuBLAS耗时10.56毫秒。

C++版本在较小矩阵上稍快，可能由于函数调用开销更低，但对于大矩阵，两者性能相当。这表明Python程序员通过CuPy，可以用简洁的代码获得与高度优化的C++/CUDA程序相近的性能。

对于半精度计算（FP16），cupy_fp16 的结果也类似：

当N=1024时，Python/CuPy耗时135微秒，C++/cuBLAS耗时50微秒。
当N=4096时，Python/CuPy耗时1.71毫秒，C++/cuBLAS耗时1.56毫秒。

这里C++版本在较小矩阵上领先优势更明显，可能因为CuPy在选择cuBLAS内核或设置数学模式时有额外开销，当执行时间很短时，这部分开销相对更显著。但整体上，CuPy仍然能够利用Tensor Core实现显著的性能提升，在N=4096时达到约80 TFLOPS，接近C++版本的87 TFLOPS。

此外需要注意设置 LD_LIBRARY_PATH 以在HPC模块环境中正确找到CUDA库（如 libcublas.so.12）。在高性能计算系统中，库路径可能比较复杂，手动指定库路径是确保CuPy和JAX等库能够正确链接依赖项的常见步骤。

JAX

JAX是一个由谷歌开发的库，它提供了类似NumPy的API，但其核心特性是一个函数转换系统，其中最重要的功能是即时编译（jit）。当使用JAX的NumPy API（jax.numpy）编写函数时，JAX并不会立即执行，而是先跟踪操作以构建计算图。在第一次调用被 @jax.jit 装饰的函数时，JAX会将计算图发送给XLA（加速线性代数）编译器。XLA编译器会进行一系列优化，例如操作融合、内存布局优化，并生成高效的机器码（例如CUDA内核）。编译后的函数会被缓存，后续调用将直接执行优化后的代码，开销很小。

基准测试代码正确地使用了这一特性：

import jax
# 在初始化时编译一次
self._matmul_jit = jax.jit(self.jnp.matmul)
# 在计时循环中调用
result = self._matmul_jit(a_jax, b_jax)
result.block_until_ready()  # 等待计算完成

基准测试在计时前进行了显式的JIT预热，以避免将编译时间计入性能测量。

JAX对多设备计算也提供了良好支持。代码中初始化了一个 PositionalSharding 对象，用于指定如何在可用设备间分布数组。在测试中，SLURM脚本请求了2个GPU，因此JAX会自动将工作分配到这两个GPU上。虽然代码中的分片设置 sharding.reshape((-1, 1)) 看起来是按行将数据分布到一维设备网格上，但 jnp.matmul 的实现能够处理这种情况并执行并行矩阵乘法。与需要手动设置的MPI或NVSHMEM相比，这种方式使得将计算扩展到多GPU变得更为简单。

我们来看JAX在2个GPU上的性能数据（来自 py.json）：

对于 jax_fp32，当N=4096时，平均时间为9.76毫秒，计算性能约为14 TFLOPS。
对于 jax_fp16，当N=4096时，平均时间为4.19毫秒，计算性能约为32.7 TFLOPS。

与其他结果对比：

单个GPU上的CuPy FP32在N=4096时耗时10.49毫秒（约13 TFLOPS）。JAX在两个GPU上的墙钟时间略快（9.76毫秒），但总吞吐量并未翻倍，这表明多GPU执行存在开销，或者问题规模不足以实现完美的扩展。
对于FP16，单个GPU上的CuPy耗时1.71毫秒（约80 TFLOPS），而JAX在两个GPU上耗时4.19毫秒，反而更慢。这表明对于这个具体的问题规模，JAX的数据分片和GPU间通信开销超过了使用第二个GPU带来的收益。block_until_ready() 确保了计时准确。JAX在一维设备网格上对 matmul 的默认并行策略可能对于这个硬件拓扑和问题规模并非最优，或者Python层面的调度开销较大。这个例子说明，性能是算法、框架、问题规模和硬件拓扑共同作用的结果，直观的假设（例如“两个GPU总比一个快”）不一定成立。

总结

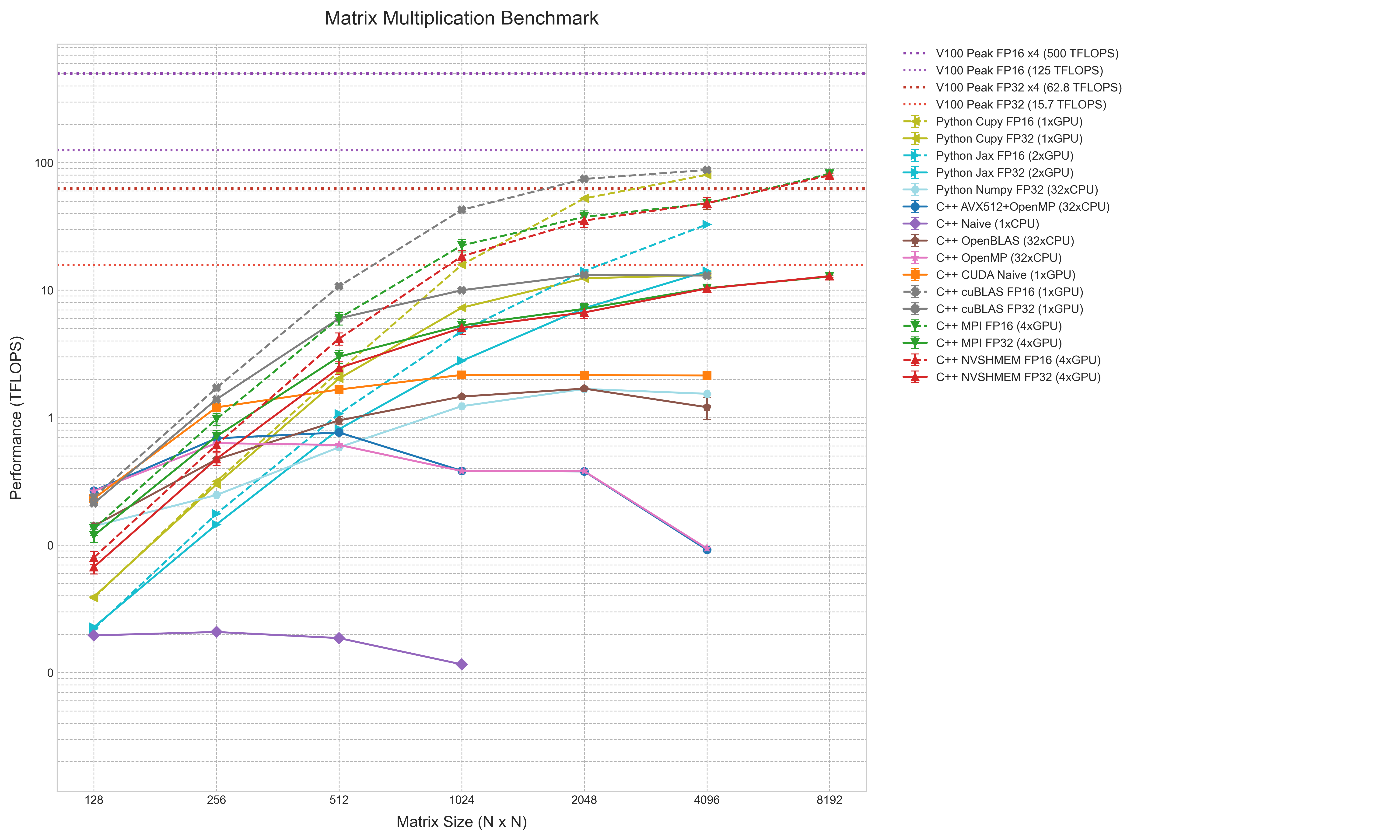
性能测试的结果最终通过一张综合图表来呈现。该图表将不同实现（从朴素的C++循环到多GPU分布式计算）的性能数据汇总在一起，并以TFLOPS（每秒万亿次浮点运算）作为统一的比较指标。

图表采用对数-对数坐标，横轴为矩阵大小（N），纵轴为性能（TFLOPS）。这种表示方法能清晰展示性能跨越多个数量级的变化。图中，不同实现方法通过颜色和线型区分，例如FP16精度的结果使用虚线。误差棒表示95%的置信区间。此外，图表中添加了代表V100 GPU在FP32和FP16精度下理论峰值性能的水平参考线，以及4-GPU系统的理论峰值线。

从图表中可以直观地看到性能的层次结构。位于最底部的是C++ Naive (1xCPU)线，其性能低于0.1 TFLOPS，且不随问题规模增大而提升，体现了单核标量计算的瓶颈。

在其之上，是多核CPU实现的性能线簇，包括C++ OpenMP、C++ AVX512+OpenMP和Python NumPy。它们的性能聚集在1-2 TFLOPS区间。C++ OpenBLAS线略高于其他，显示了高度优化库的优势。

GPU实现的性能线则处于更高的位置。即便是未优化的C++ CUDA Naive实现，其性能也超过了所有CPU结果，最高超过2 TFLOPS。采用cuBLAS库的FP32实现（包括C++和Python CuPy）以及4-GPU的MPI实现，性能在10-15 TFLOPS区间，接近但未达到单V100的FP32理论峰值。Python JAX FP32 (2xGPU)也位于此区域，其性能并未达到单GPU的两倍。

图表顶端是FP16精度的性能线，包括C++ cuBLAS FP16、Python CuPy FP16以及多GPU的MPI/NVSHMEM FP16。它们的性能显著更高，4-GPU分布式计算在N=8192时达到约80 TFLOPS，接近单V100的FP16理论峰值。Python JAX FP16 (2xGPU)的性能线明显低于其他FP16实现。

这张图表综合展示了从简单实现到充分利用硬件特性的优化所带来的性能差异，并直观反映了不同计算平台（多核CPU、单GPU、多GPU）和精度选择（FP32、FP16）对矩阵乘法效率的影响。

Barkla2 HPC#

朴素算法#

OpenMP#

OpenMP+SIMD#

OpenBLAS#

朴素CUDA#

cuBLAS#

MPI + cuBLAS#

NVSHMEM#

NumPy#

CuPy#

JAX#

总结#